El Interés Compuesto

El interés compuesto es uno de los conceptos más poderosos en el mundo de las finanzas. Albert Einstein lo llamó «la fuerza más poderosa del universo», y por buenas razones. No solo es fundamental para comprender cómo crecen las inversiones, sino que también tiene un impacto significativo en la creación de riqueza a lo largo del tiempo. En este artículo, exploraremos en profundidad qué es el interés compuesto, cómo funciona, sus efectos a largo plazo, cómo calcularlo, y cómo se diferencia del interés simple.

¿Qué es el Interés Compuesto?

El interés compuesto es el proceso mediante el cual el interés ganado o pagado sobre un capital inicial se suma al capital, de modo que en los periodos siguientes, el interés se calcula sobre el capital inicial más los intereses acumulados. En otras palabras, es el «interés sobre el interés», lo que significa que el dinero tiene el potencial de crecer exponencialmente con el tiempo.

Por ejemplo, si inviertes €1.000 en una cuenta que ofrece un interés compuesto anual del 5%, al final del primer año tendrás €1.050. En el segundo año, el 5% se aplicará sobre los €1.050, no solo sobre los €1.000 iniciales, lo que resulta en €1.102,50 al final del segundo año.

La Fórmula del Interés Compuesto

La fórmula para calcular el interés compuesto es fundamental para entender cómo funciona este fenómeno. La fórmula general es:

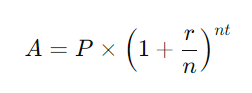
Donde:

• A es el monto total acumulado, incluyendo el interés.
• P es el capital inicial (la cantidad de dinero que se invierte o presta inicialmente).
• r es la tasa de interés anual (expresada como decimal).
• n es el número de veces que se capitaliza el interés por año.
• t es el tiempo que el dinero se invierte o presta, en años.

Ejemplo de cálculo:

Imaginemos que inviertes €5.000 a una tasa de interés anual del 4%, capitalizada mensualmente, durante 10 años. Aplicando la fórmula, tendríamos:

A = 5000 ( 1 + [0,04/12] ) ^ ^(12×10)

A = 5000 ( 1 + 0,0033 ) ^ ¹²⁰

A ≈ 5000 × 1, 48886 = 7.444,30

Esto significa que al final de los 10 años, tu inversión inicial de €5.000 habría crecido a aproximadamente €7.444,30.

Diferencia entre Interés Compuesto e Interés Simple

Para comprender completamente el poder del interés compuesto, es crucial compararlo con el interés simple. El interés simple es el tipo de interés que se calcula únicamente sobre el capital inicial, sin tener en cuenta los intereses acumulados en periodos anteriores. La fórmula del interés simple es:

I = P × r × t

Donde:

• I es el interés ganado.
• P es el capital inicial.
• r es la tasa de interés anual.
• t es el tiempo en años.

Ejemplo de cálculo de Interés Simple

Tomando el mismo ejemplo anterior, si inviertes €5.000 a una tasa de interés anual del 4% durante 10 años, usando el interés simple, el cálculo sería:

I = 5000 × 0,04 × 10

I = 2000

El interés simple te daría €2.000 en 10 años, lo que sumado a tu capital inicial resultaría en €7.000. Esto es menos que los €7.444,30 que obtendrías con el interés compuesto.

Comparación

La principal diferencia radica en cómo se calcula el interés. En el interés simple, el interés no se capitaliza; se calcula solo sobre el capital inicial. Esto significa que el crecimiento de la inversión es lineal. En el interés compuesto, el interés se capitaliza y se añade al capital inicial, lo que significa que en cada periodo el interés se calcula sobre un capital mayor, lo que resulta en un crecimiento exponencial.

¡Muy importante esto! Si estamos invirtiendo y queremos beneficiarnos del Interés Compuesto, debemos reinvertir las ganancias que hayamos obtenido. En caso contrario, estaríamos en una situación de Interés Simple. Si estás inviritiendo en Fondos de Inversión fíjate en esto: Deben tener indicado que son de «Acumulación» lo que significa que las ganancias se reinvierten automáticamente adquiriendo participaciones nuevas del Fondo en el que estamos invirtiendo. Esto es Interés Simple.

Vamos a verlo con un ejemplo. El gráfico de debajo se ha preparado bajo los siguientes supuestos: €5.000 de capital inicial, tasa de interés del 8%, capitalización anual y horizonte temporal de 25 años. Veamos la diferencia entre la curva de Interés Compuesto e Interés Simple.

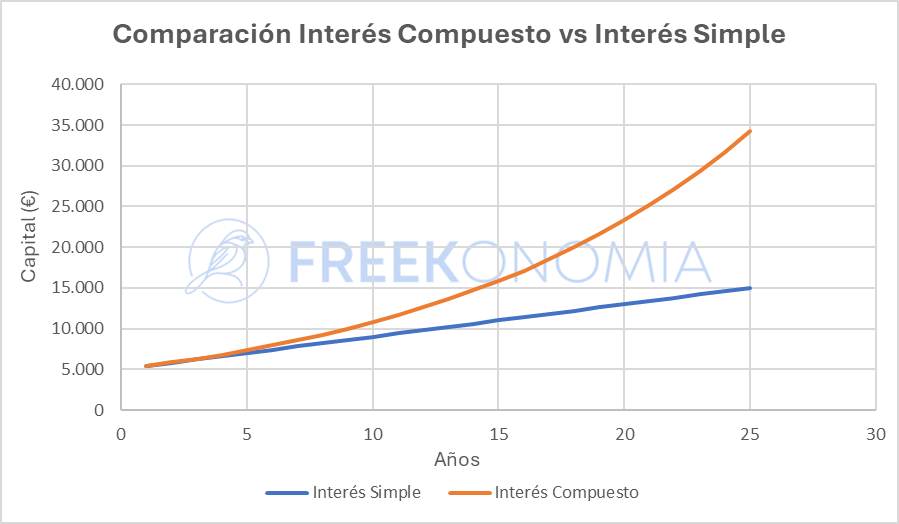
En el ejemplo presentado podemos ver claramente como la curva de Interés Compuesto es exponencial y crece de esta forma a medida que pasan los años, mientras que la de Interés Simple es una curva que se mantiene lineal durante toda la vida de la inversión.

Efectos a Largo Plazo del Interés Compuesto

El interés compuesto puede tener un efecto dramático a largo plazo. Cuanto más tiempo dejes que tu dinero crezca, más significativo será el impacto del interés compuesto. Esta es la razón por la cual los expertos financieros enfatizan la importancia de empezar a ahorrar e invertir lo antes posible.

Ejemplo de duración en el tiempo

Supongamos que dos personas, Ana y Luis, deciden ahorrar para su jubilación. Ana comienza a ahorrar €200 al mes a los 25 años, mientras que Luis comienza a ahorrar la misma cantidad a los 35 años. Ambos obtienen una tasa de interés compuesto anual del 6%.

Para cuando Ana y Luis cumplen 65 años, Ana habrá ahorrado €96.000 en total, mientras que Luis habrá ahorrado €72.000. Sin embargo, debido al interés compuesto, Ana tendrá aproximadamente €430.000, mientras que Luis tendrá alrededor de €240.000. La diferencia de €190.000 se debe simplemente a que Ana comenzó a invertir 10 años antes, permitiendo que el interés compuesto hiciera su magia durante un periodo más largo.

El Efecto de la Frecuencia de Capitalización

La frecuencia con la que se capitaliza el interés (anualmente, semestralmente, trimestralmente, mensualmente o diariamente) puede tener un impacto significativo en la cantidad final acumulada. Cuanto más frecuentemente se capitalice el interés, mayor será el monto final, debido a que el capital se actualiza con mayor frecuencia y cada actualización incluye los intereses más recientes.

Si tomamos una inversión de €1.000 a una tasa de interés del 8% durante 5 años, podemos ver cómo varía el monto final según la frecuencia de capitalización:

• Anual: 1.000 x ( 1 + [0,08/1]) ^ (1/5) = €1.469,33
• Semestral: 1.000 x ( 1 + [0,08/2]) ^ (2/5) = €1.480,24
• Trimestral: 1.000 x ( 1 + [0,08/4]) ^ (4/5) = €1.486,06
• Mensual: 1.000 x ( 1 + [0,08/12]) ^ (12/5) = €1.491,33
• Diaria: 1.000 x ( 1 + [0,08/365]) ^ (365/5) = €1.493,27

Como se puede observar, la diferencia no es gigantesca, pero sí significativa, especialmente cuando hablamos de grandes sumas de dinero y plazos más largos.

Aplicaciones del Interés Compuesto

No solo es relevante para inversiones a largo plazo; también tiene aplicaciones en una variedad de situaciones financieras cotidianas.

1. Cuentas de Ahorro: Muchas cuentas de ahorro en bancos utilizan el interés compuesto para calcular el interés sobre los depósitos. Aunque las tasas de interés pueden ser bajas, el efecto que nos otorga puede hacer que los ahorros crezcan de manera más efectiva que si solo se aplicara un efecto simple.
2. Inversiones en Bolsa: El interés compuesto es clave en el crecimiento de inversiones en acciones, bonos y fondos mutuos. A medida que los dividendos y los intereses se reinvierten, el valor de la inversión puede crecer exponencialmente.
3. Préstamos y Deudas: También se aplica a deudas, como las tarjetas de crédito y préstamos. Si no pagas tu saldo completo cada mes, los intereses se suman al capital adeudado, lo que puede hacer que la deuda crezca rápidamente.
4. Planes de Retiro: Los planes de jubilación, como los 401(k) en Estados Unidos, dependen del interés compuesto para crecer a lo largo de las décadas. Las contribuciones constantes, junto con el con este efecto, pueden convertir pequeñas sumas en un fondo considerable para la jubilación.

Estrategias para Aprovechar el Interés Compuesto

Dado que el interés compuesto puede tener un impacto tan poderoso en la creación de riqueza, es esencial aprovecharlo de la manera correcta. Aquí hay algunas estrategias para maximizar los beneficios:

1. Comenzar Temprano: Cuanto antes comiences a invertir o ahorrar, más tiempo tendrá tu dinero para crecer a través del interés compuesto. Incluso si puedes aportar solo pequeñas cantidades al principio, el tiempo será tu mejor aliado.
2. Reinvertir las Ganancias: Una de las claves para aprovechar el interés compuesto es reinvertir cualquier ganancia que obtengas, ya sean dividendos, intereses o rendimientos de capital. De esta manera, tus ganancias generarán más ganancias.
3. Contribuir Regularmente: Realizar contribuciones regulares, ya sea mensual o anualmente, puede potenciar el efecto del interés compuesto. Incluso si no puedes invertir grandes sumas de una sola vez, las contribuciones consistentes pueden acumularse significativamente con el tiempo.
4. Evitar Retiradas Tempranas: Retirar dinero de una inversión antes de tiempo puede interrumpir el proceso de interés compuesto y reducir significativamente el crecimiento a largo plazo.

Conclusión

El interés compuesto es una herramienta financiera poderosa que, cuando se utiliza correctamente, puede ayudarte a construir una considerable cantidad de riqueza a lo largo del tiempo. A diferencia del interés simple, que ofrece un crecimiento lineal, el interés compuesto tiene el potencial de hacer que tus inversiones crezcan de manera exponencial, debido a la capitalización del interés ganado.

Comprender cómo funciona, la fórmula para calcularlo y las diferencias con el interés simple es fundamental para cualquier persona que desee tomar decisiones financieras informadas. Ya sea que estés ahorrando para la jubilación, invirtiendo en la bolsa o simplemente tratando de hacer crecer tus ahorros, este efecto debería ser una parte central de tu estrategia financiera.

Recuerda, el tiempo es el mayor aliado del interés compuesto, por lo que empezar temprano y ser constante en tus inversiones son claves para maximizar su poder.